Snow metamorphism transforms the structure of fresh fallen snow within a very short time. For several years now we have been able to observe and measure these changes as they occur with the aid of a computed tomography (CT) scanner.
As a 'hot' material, snow is highly mutable, and because its temperature is always close to its melting point, it also has a high vapour pressure. As a consequence, ice is constantly vaporising without passing through the liquid phase (sublimation), and the water vapour is then deposited on a slightly colder surface. The speeds at which the transformation processes (metamorphism) take place vary enormously, depending on the ambient conditions. As a general rule, the higher the temperature and the greater the temperature differences, the more rapidly the snow structure changes.
The properties of the snow also change as it undergoes metamorphism. Understanding how and why metamorphism occurs is thus very important for all those who are interested in the science of snow, including those investigating its mechanical and physical properties, changes in the snowpack, the process of avalanche-forming, the ice cover in the polar regions, or various climate models, for example. The ability to observe snow with a CT scanner has enabled us to make significant advances in examining and quantifying the relevant processes. We can now observe transformations as they occur in snow samples in controlled ambient conditions (e.g. pre-defined temperature or temperature gradient), and measure the properties that interest us (such as density, specific surface area, anisotropy etc.) at any time.
Isothermal metamorphism
If the same temperature prevails on the snow surface as on the ground, metamorphism (in this case isothermal) takes place very slowly. The driving force is the physical 'attempt' to reduce the surface area. During this process the ice structures on the convex ends of the tiny ice branches, where surface tension is highest, sublimate and the water vapour is then deposited in concave depressions. The originally star-shaped crystals thereby adopt a more rounded form (Fig. 1). Such isothermal temperature conditions occur in nature in the polar regions at a depth of several metres below the surface and in other very deep snowpacks.
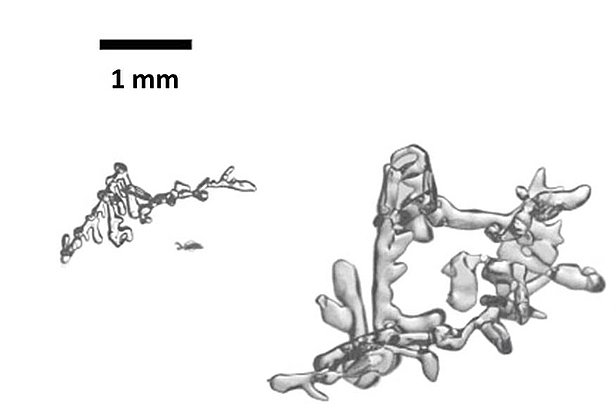
Temperature gradient metamorphism
Outside of the polar regions, snowpacks are generally seasonal and tend to be relatively shallow. Whereas the surface of these snowpacks is constantly influenced by the atmospheric temperature, the temperature on the ground beneath the snowpack remains at fairly constant 0° C. The temperature gradient has the effect of initiating migration of the water vapour in the interstices of the ice from warm to cold – in the Alpine snowpack, from the ground upwards. When the water vapour encounters an ice crystal, it is deposited on the crystal's underside, and the crystal starts to grow downwards. At the same time, sublimation occurs on the crystal's warmer top surface and thus produces fresh vapour to feed the crystal situated above it. Over time, this process completely renews and transforms the original ice crystals. The reconstituted, typically cup-shaped crystals (Fig. 2) are unlike those that form naturally in clouds.
The following film, which illustrates the formation of depth hoar, was produced from time-lapse images captured by the CT scanner. The conditions in the CT scanner replicated those that can occur for brief periods in nature, in this case a temperature gradient of 5° C per 10 cm.
Variable temperature gradients
In the snowpack both the temperature gradient and the direction of the gradient can change. In other words, the snowpack is sometimes warmer on the surface than below the surface, but the situation can be reversed within just a few hours. By conducting experiments with the CT scanner we analysed how the change in direction of the temperature gradient influences the snow metamorphism. Reflecting the conditions that occur on clear winter days at a depth of around 10 cm, fresh snow was exposed to an alternating temperature gradient of ± 9° C per 10 cm. Within 12 hours, 60% of the snow mass had been transformed.
This recrystallisation process gave rise to larger and less coherent snow structures. The snow crystals were transformed into arm-like rounded shapes and were not at all faceted even after 14 days.
Melt metamorphism
Melt metamorphism is a particular manifestation of isothermal metamorphism. As temperature increases, the air in the pore space between snow crystals is replaced by melt water at a temperature of 0° C. Since heat is transferred much more swiftly in liquid water than in pore space, the transformation into large rounded structures occurs much more quickly.